Basic scanning
Look at the grid, bearing in mind the fundamental rule that each row, column and 3×3 box must contain one instance only of each of the digits from 1 – 9. The other side of this is that if a digit is already in a row, column, or 3×3 box, it can’t appear again in that particular row, column, or 3×3 box.
Many of these techniques are dependent on your writing in the possible digits (these are called candidates) for every cell.
So keep the score – write in the possible candidates for each cell and keep scanning for helpful patterns. When you add a digit which you know is correct, make sure you remove that digit from any candidate notes for the other cells of its row, column and 3×3 box.
Singles
Naked Single
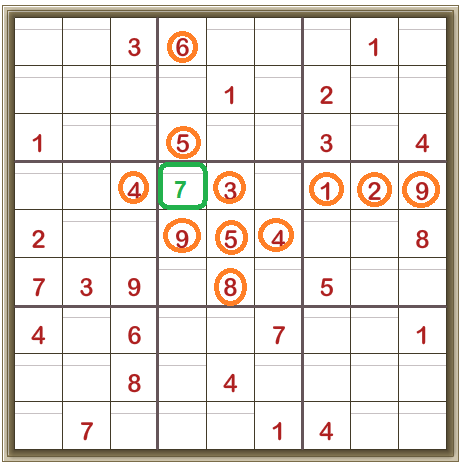
Looking at the cell outlined in green.
It can’t be 1, 2, 3, 4 or 9 as these digits already appear in the same row.
It can’t be 5, 6, or 9 as these digits already appear in the same column.
It can’t be 3, 4, 5, 8, or 9 as these digits already appear in the same 3×3 box.
Combining this information, it can’t be 1, 2, 3, 4, 5, 6, 8, or 9.
Therefore, it must be 7.
Hidden Singles
There’s a 2 in the top row, in the top right-hand 3×3 box.
There’s a 2 in the second row in the top middle 3×3 box.
So the only place left for a 2 in the top left-hand 3×3 box is where it is shown in green.

Single Position
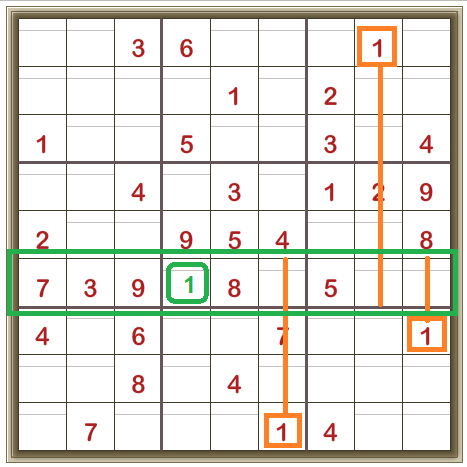
We’re looking at the sixth row down from the top.
Consider digit 1.
It can’t be in the last column as there’s a 1 in that column already.
It can’t be in the second-last column as there’s a 1 in that column already.
It can’t be in the fourth-last column as there’s a 1 in that column already.
So the only space left for the digit 1 is shown in green:
Another Single Position example
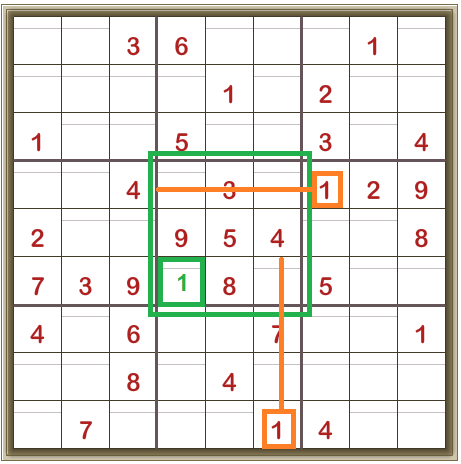
Here’s another example from the same puzzle, looking at the centre 3×3 box.
Consider digit 1.
It can’t be in the top row of the 3×3 box as there’s already a 1 in that row.
It can’t be in the right-hand column of the 3×3 box as there’s already a 1 in that column.
So the only cell left for the digit 1 is the one shown in green below:
Moving on
Naked Pairs
Here we’re looking at the centre row. In the two unfilled cells on the right, both must be either 5 or 8.
So 8 can’t be anywhere else in this row.
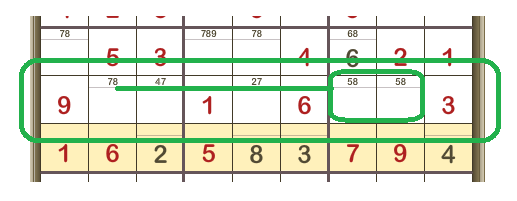
Therefore, we can remove the candidate 8 from the second cell from the left. (Its only remaining candidate is the 7 so now we know this cell contains 7).

Naked Triples and Quads
Looking at the 3×3 box (LH, middle)
The three circled cells have their candidates ‘pencilled’ in. 147, 14, and 147.
This means that ONLY 1, 4 or 7 can appear in these three cells within this 3×3 box.
So, 1, 4, and 7 CANNOT appear in any of the other cells in this 3×3 box.

So in the cells outlined in green below, we can remove the candidates 1, 4, and 7

Giving:

Naked quads are much less frequently found, but follow the same principle.
Hidden Pairs
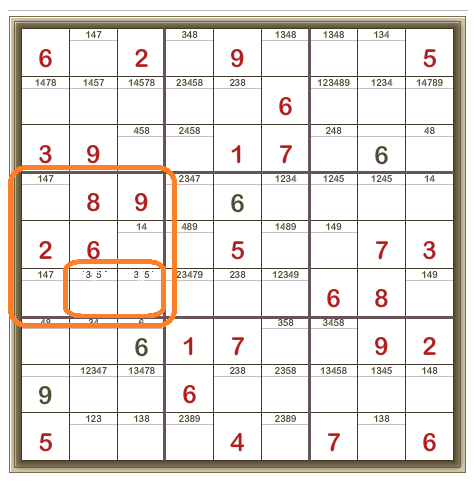
Now we’re looking at the 3×3 box in the middle of the left column.
Looking closely, you can see the two cells outlined in orange are the ONLY two cells in this 3×3 box for which the digits 3 and 5 are candidates.
This is a Hidden Pair and what it means is that we can remove the other candidates (1, 4, and 7) from these cells

Giving:
Aside
Note that the presence of a Hidden Pair implies the presence of a Naked or Hidden group in the other cells within this 3×3 box. In this example the 2, 6, 8, and 9 are givens.
We’ve discovered that the two bottom right cells must either be 3 or 5.
So the remaining three cells must contain 1, 4, and 7.
Hidden Quads
Look at this row:
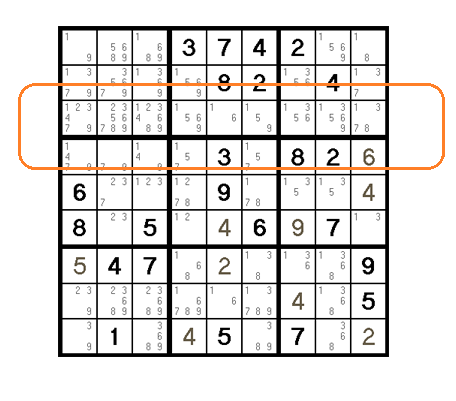
In the five cells selected, only the candidates 1,3,5,6 and 9 appear.

So 1,3,5,6 and 9 CANNOT be in any other cells in this row.
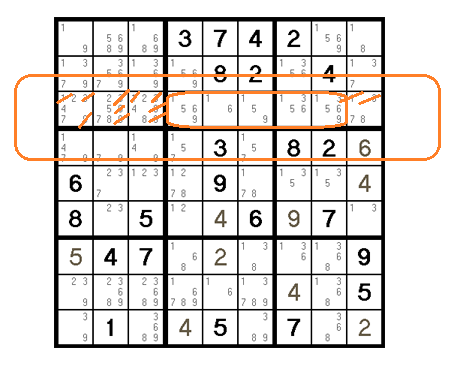
Revealing the hidden quad of 2,4,7 and 8.

‘Not’ options
Pointing Pairs 1
This technique might not tell where a particular digit IS, but it may show clearly where that digit ISN’T.
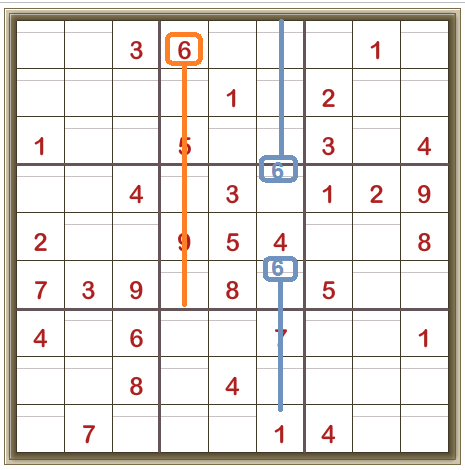
Consider the centre 3×3 box and the digit 6.
The digit 6 can’t be in the left-hand column of the centre 3×3 box, as there’s already a 6 in that column (orange line).
The 6 can’t be in the middle column of the centre 3×3 box, as all three cells are givens (3,5, and 8 respectively).
So the 6 HAS TO be in the right-hand column of the centre 3×3 box, in one of the two unfilled cells. And that means that the digit 6 can’t be anywhere else in that column (blue lines).
Aside
Now look at the 3×3 box in the middle at the bottom (green outline) from the example above.
The digit 6 can’t be in the left-hand column of the 3×3 box as there’s already a 6 in that column (orange line).
The digit 6 can’t be in the right-hand column of the 3×3 box (green outline) as we’ve just shown that, in that column, the digit 6 has to be in the middle 3×3 box (blue lines).
And we can see that the digit 6 can’t be in the top row of the 3×3 box outlined in green as there’s already a 6 in that row (another orange line).
So the only place left in the 3×3 box outlined in green is the position shown in green below:
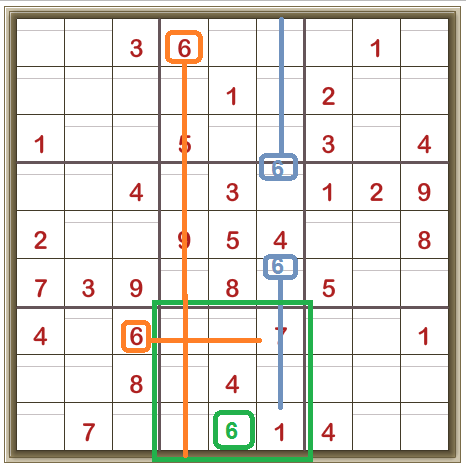
You won’t always get a definite cell placement from a Candidate Lines instance, but it’s nice when you do. (We’ve used the Locked Candidates technique here).
More Pointing Pairs/Triples

The candidates have been added to each cell in this detailed view.
In the top 3×3 box, the 2 appears in only two cells, both in the same column. The 2 MUST be in one of these two cells.
So, it can’t be anywhere else in that column and we can remove it from the candidates in the bottom cell of the middle 3×3 box.
Every little helps…
Box/Line reduction
This is where we compare the rows and columns with the 3×3 boxes and see what turns up.
In the third row of this Sudoku, the digit 5 appears as a candidate ONLY in the last two cells of the row. So the 5 MUST be in one or other of these two cells. But both of these cells are also in the right top 3×3 box.
Thus the 5 CANNOT be anywhere else in that 3×3 box.

And we can cross out that 5 candidate:

Expert
X-Wings
Why X-Wings? Because the pattern relies on the cells shown in green and they form an X pattern. These patterns emerge after you’ve used all the easier techniques and carefully checked the candidates.
In the fourth row there are only two cells in which 6 is a candidate.
In the eighth row, there are only two cells in which 6 is a candidate.
AND these cells are also in the same two columns.
So 6 MUST be in each of these columns but can ONLY be in two of these four cells.
And so 6 can be removed as a candidate from any other cell in both these columns

Giving:
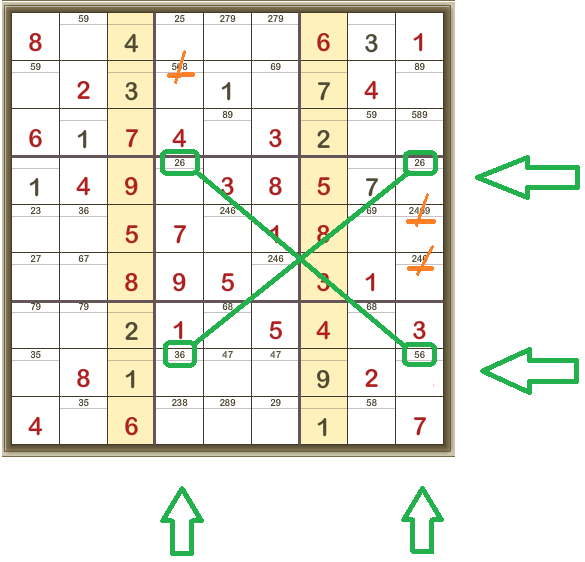
The X-Wing doesn’t solve the values in the four cells of the X-Wing. It tells you where a candidate CANNOT be.
Aside
Using colour to display what happens in the X-Wing, you can see that no matter what the solution is, the 6 MUST be in one of the green cells in each of the two columns.
Look at the four green sets of candidates. Each can only be one of two choices.
In Blue and in Pink are the only two sets of possibilities. In BOTH cases, there will be a 6 in one of the X-wing cells in the fourth column from the left AND in one of the X-wing cells in the column on the right. We don’t know which of the X-wing cells the 6 will be in but we DO know that 6 can’t be in any other cell in the fourth column OR in any other cell in the column on the right.

Simple Colouring (Solving with Colours)
We’re looking for pairs – one candidate number with only two potential positions in a row, column or 3×3 box.
In this case, it’s pairs of 7s.
In each pair, either one position OR the other will be 7. So we can colour the pairs to indicate the on/off options for digit 7.
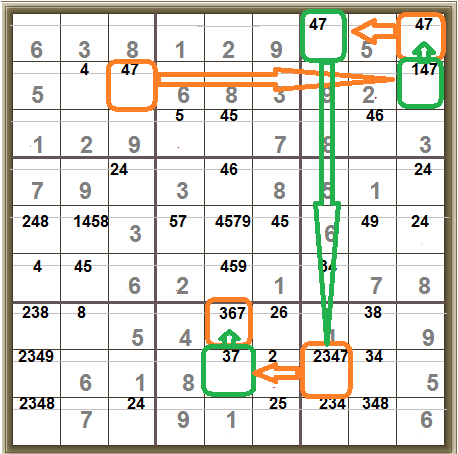
Then, remembering that only one place in each 3×3 box can have a 7, we now know that the 7 MUST be in the top right-hand cell.
Now we can work through the chain in either direction to get a lot of positions where the 7 has to be.
Note: this ONLY tells you about the 7s. AND you won’t always get an exact value for any cell, just a pattern of on/off for 7s in the grid.
In detail:

We established an on/off pattern for the digit 7. Now look at this 3×3 box. In it are two cells, both the same colour, green.
Option One: both green cells have to be ‘off’ (not 7), in which case the orange cell in this 3×3 box MUST BE ‘on’ and therefore it must be 7.
Option Two: both green cells have to be ‘on’ in which case both have to be the digit 7 – but this cannot be – 7 can only appear once in each 3×3 box.
So Option Two cannot be correct and therefore Option One MUST be correct and so the top right hand cell MUST be 7.
And thus we can establish all of these:
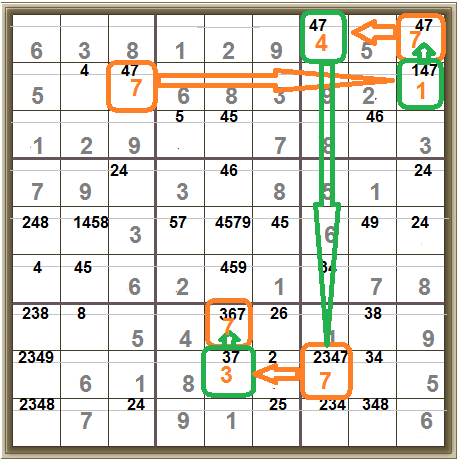
Y-Wing
What you are looking for is this pattern, three cells with only two candidates each and in which the candidate numbers form the pattern AB, BC and AC, and a fourth cell in which C is a candidate number. The cells have to share rows/columns as shown below.
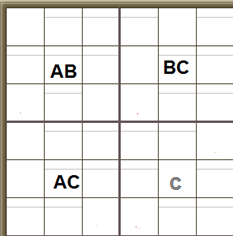
We’ve got one cell with only two candidates, A or B, and it’s in the same row as another cell with only two candidates, B and C. And it’s in the same column as another cell with only two candidates, A and C.
The fourth cell has C as a candidate (there will be at least one other candidate in this cell).

If the top cell is A, the cell below it must be C. So nothing else in its row may be C.
If the top cell is B, the cell across from it must be C. And nothing else in its column may be C.
So we can see that, whether the first cell has the value A or B, the C cannot be in that cell in the bottom-right corner.
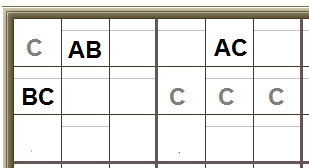
It works within the 3×3 boxes, too.
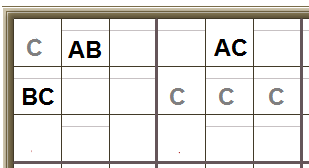
We’ve got one cell with only two candidates, A and B. It’s in the same row as another cell with only two candidates, A and C. And it’s in the same 3×3 box as another cell with only two candidates, B and C. In this example there are several other cells which also have the candidate C (these cells will have other candidates, too).
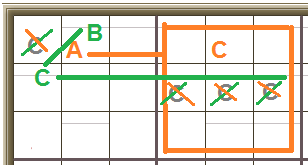
If the top cell is A, the cell across from it must be C, so nothing else in its row or 3×3 box can be C.
If the top cell is B, the other cell in its 3×3 box must be C, and nothing else in its row or 3×3 box can be C.
Again, whether that first cell has the value A or B, we can see where the value C CANNOT be.
The tricky bit is spotting these patterns when all the cells are cluttered up with many candidate numbers. Look for the pairs!
Detail of Y-Wing including 3×3 box
Option One:

The cell can be A or B. Let’s call it A. If it is A then the cell AC in the same row MUST be C.
So we can cross out or remove all the C candidates as shown.
Option Two:

Option Two:
The cell can be A or B. Let’s call it B. If it is B then the cell BC in the same 3×3 box MUST be C.
So we can cross out or remove all the C candidates as shown.
BUT the crossing-out of the C candidates is exactly the same for BOTH options. And so although we still don’t know the values of the AB, AC and BC cells, we DO know that C cannot be a candidate in the cells where C is crossed-off in both options.
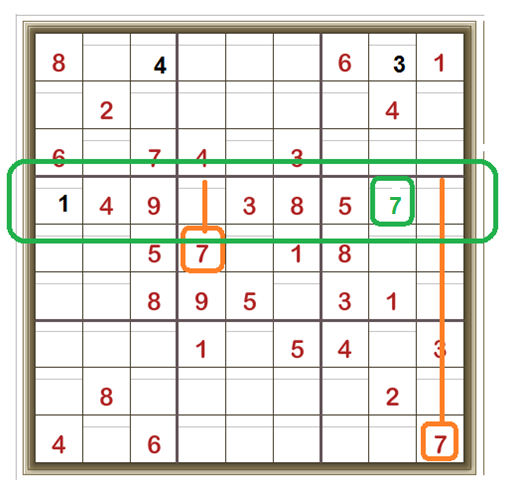
Swordfish
Where an X-Wing works with two pairs of cells, a Swordfish works with three.
That is, in three rows, the two cells that a particular candidate digit can be are in the same three columns as each other, too. This is also called a closed loop.
By steps then:
Look at all the cells in which 5 is a candidate.

And identify the THREE rows in which the 5 can only be in one of TWO cells AND two of each of these cells fall in only THREE columns:
And now you can cross of the 5 in the middle left-hand cell in the top middle 3×3 box:
It looks like a roundabout way to eliminate that 5 but, once again, every little helps.
(Note: you may have found Y-Wings in this puzzle, first)
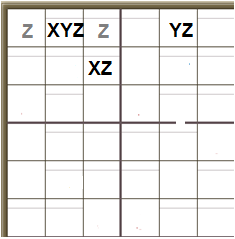
XYZ Wing
Look at the pattern of candidate numbers. One cell has the candidates XYZ. One cell on the same row as it has the candidates YZ. AND one cell within its 3×3 box has the candidates XZ.
Two other cells in the same row as the XYZ cell have the candidate Z (they will have at least one other candidate, too):

Option One
Assume the XYZ cell has the value X. Then the other cell in its 3×3 box must be Z. So no other cell in that 3×3 box can be Z and we can cross off those candidates.

Option Two
Assume the XYZ cell has the value Y. Then the other cell in its row must be Z. So no other cell in that row can be Z and we can cross off those candidates.

Option Three
Assume the XYZ cell has the value Z. Then no other cell in its row (or 3×3 box) can have the value Z and so we can cross off those candidates.
In all three options, and there are only three options, the same candidates are crossed off. So we know these two cells can NEVER have the value Z.
Again, this technique may not solve any cell completely, but it will eliminate a candidate or two.
No, really?
Forcing Chains (Digit, Nishio, Cell, Unit, or Quad), Turbot fish, Jellyfish, Squirmbag, Tabling (needs computer), Empty Rectangles, Finned X-Wings and Swordfish, Death Blossom (seriously, someone online found one with six eliminations…), Sue-de-Coq, Grouped X-Cycles, and finally Guessing (Bowman’s Bingo) and Uniqueness (if the puzzle is supposed to have only one solution, one can use that to eliminate value assignments that allow multiple solutions).
To explain these would take days – try Googling.
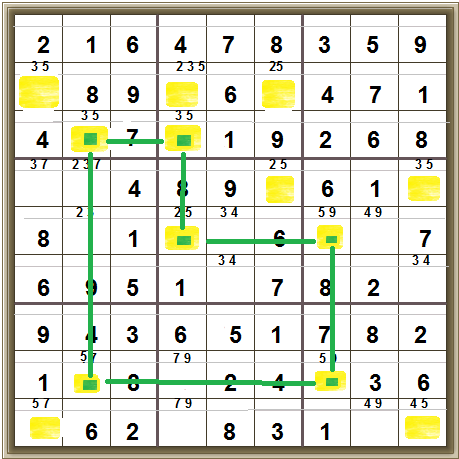
One from beginning to end

Scan carefully.
There’s only one place the 4 can be in the top-left 3×3 box:


And there’s only one place the 3 can be in the right-top 3×3 box
And there’s only one place the 1 can be in middle-left 3×3 box:

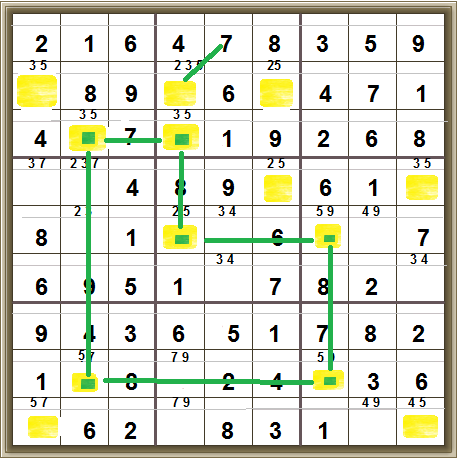
Now, in the middle row, there’s only one place where the 7 can be:
Which then leaves only one place in the top right 3×3 box where 7 can be:
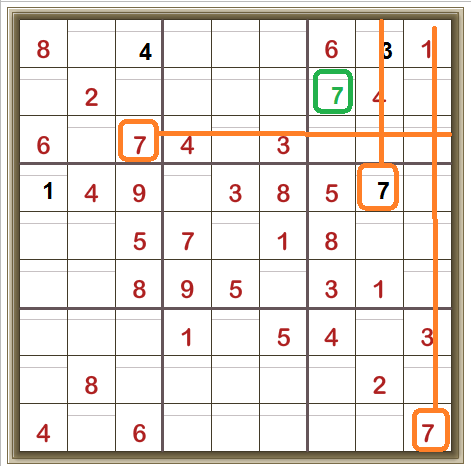

Now looking at the third column from the right, there’s only one place the 2 can be.
So that, in the third column from the left, there’s only one place for the 2 to be:

Now I’ve added all the candidate numbers, revealing a couple of naked pairs which allow us to remove some candidates:
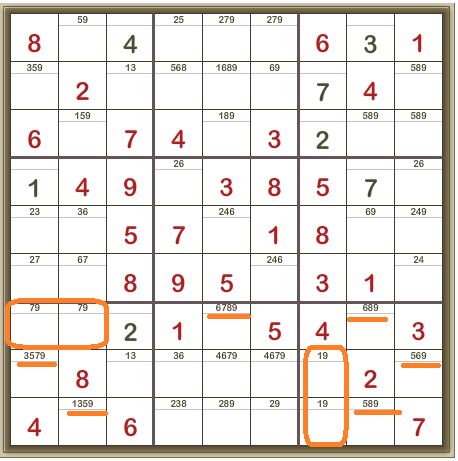
Ending up with this:

Which gives us this interesting position.
In the second last row, there are four cells with 3 and 5, 1 and 3, 3 and 6, and 5 and 6 as their candidates. This means that the digits 1, 3, 5, and 6 MUST be in these four cells and CANNOT be anywhere else in this row. And that means that we know the positions of the 9 and therefore the 1 in the bottom right 3×3 box:
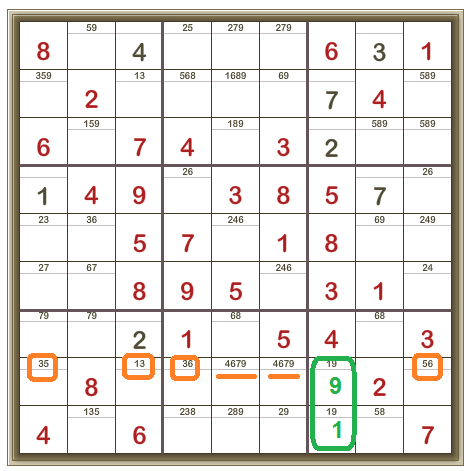
Now, we’re here (and one column is now filled with all its digits and shaded to show it’s correct).
There’s another interesting pair in the bottom-left 3×3 box. Two cells both have candidates 3 and 5. So 3 and 5 MUST be in those two cells. So 3 CANNOT be in any other cell in this 3×3 box. Thus the cell with 1 and 3 as the candidates (in the bottom-left 3×3 box) cannot have 3 and MUST be 1. This leads the cell in the top-left 3×3 box, which also has the candidates 1 and 3, to be 3 as now it cannot be 1.
Then there’s only one place left for a 1 in the top-left 3×3 box. And it follows that then there’s only one place left in the top-middle 3×3 box for its 1.

Giving this, which now has TWO correctly completed columns:

And in the second column from the right there’s a locked candidate. That is, the 8 for this column must be in the bottom 3×3 box, which means we can remove the candidate 8 up in the top-right 3×3 box:
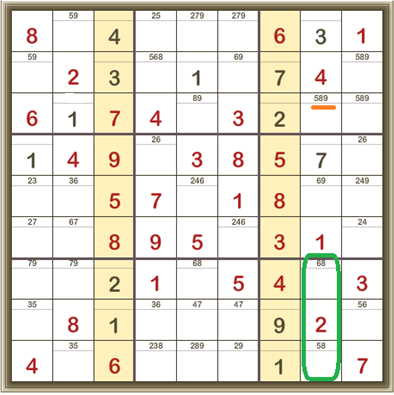
Now look at the third row from the top. The only available cells into which the 5 can go are both in the top-right 3×3 box. So that means 5 CANNOT be anywhere else in that top-right 3×3 box and we can remove 5 as a candidate from any other cell:
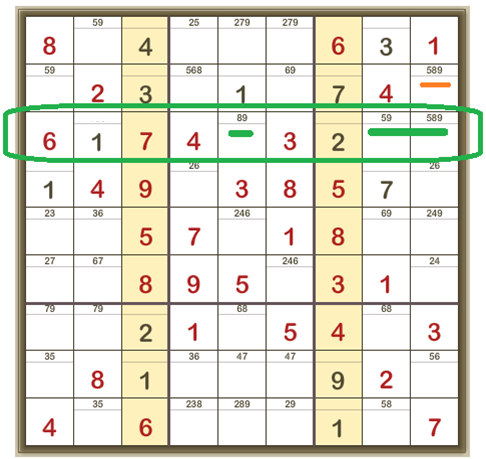
And, oh, happy day! We have an X-wing.
Only two cells in the fourth row can contain a 6.
Only two cells in the eighth row can contain a 6.
And these cells are in the same two columns as each other.
So 6 CANNOT be anywhere else in these two columns.

We can remove the 6 candidates from those cells to get this, where now the only cell in the second row which can contain a 6 is shown:
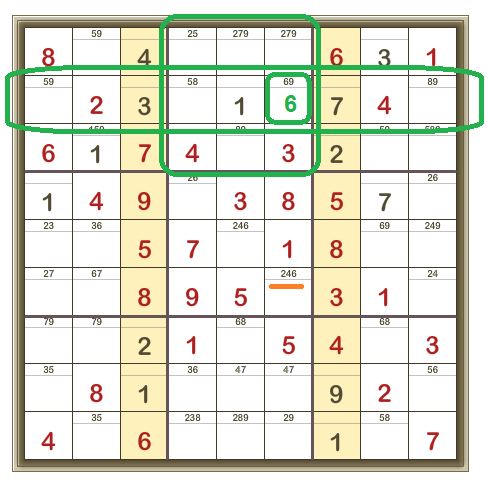
Then the only cell in the sixth row which can be 6 is shown here:

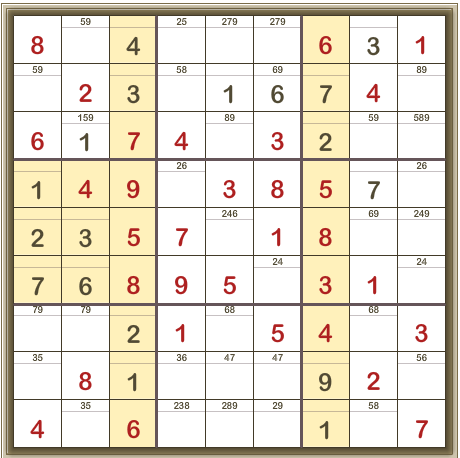
Which means that in the left middle 3×3 box, the middle cell can only be 3, and the puzzle is pretty well solved (more detail below):








Recent Comments